Like the classical AND, OR, NOT, etc... gates for classical bit, there are
Quantum Gates for QBits. We will see some examples on Quantum gates acting on a single QBit.
Small reminder of classical gates
A boolean gate is a gate taking one or several boolean values as input, and
return a boolean value.
For example, the NOT gate return 0 if input is 1 and return 1 if input is 0.
Its Truth Table is as below:
The AND gate takes 2 input bits and return one value:
| In1 |
In2 |
Out |
| 0 |
0 |
0 |
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
1 |
QBit Vector Representation
In previous article, wa have seen that a qbit can be represented using cartesian coordinates with \(\left| \Psi \right> = \alpha \left| 0 \right> + \beta \left| 1 \right>\):
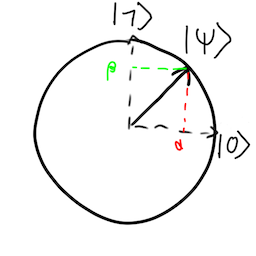
and using the Bloch Sphere and some spherical coordinates with \( \left| \Psi \right> = cos(\frac{\theta}{2}) \left| 0 \right>+ sin(\frac{\theta}{2}) e^{i\phi} \left| 0 \right>\)
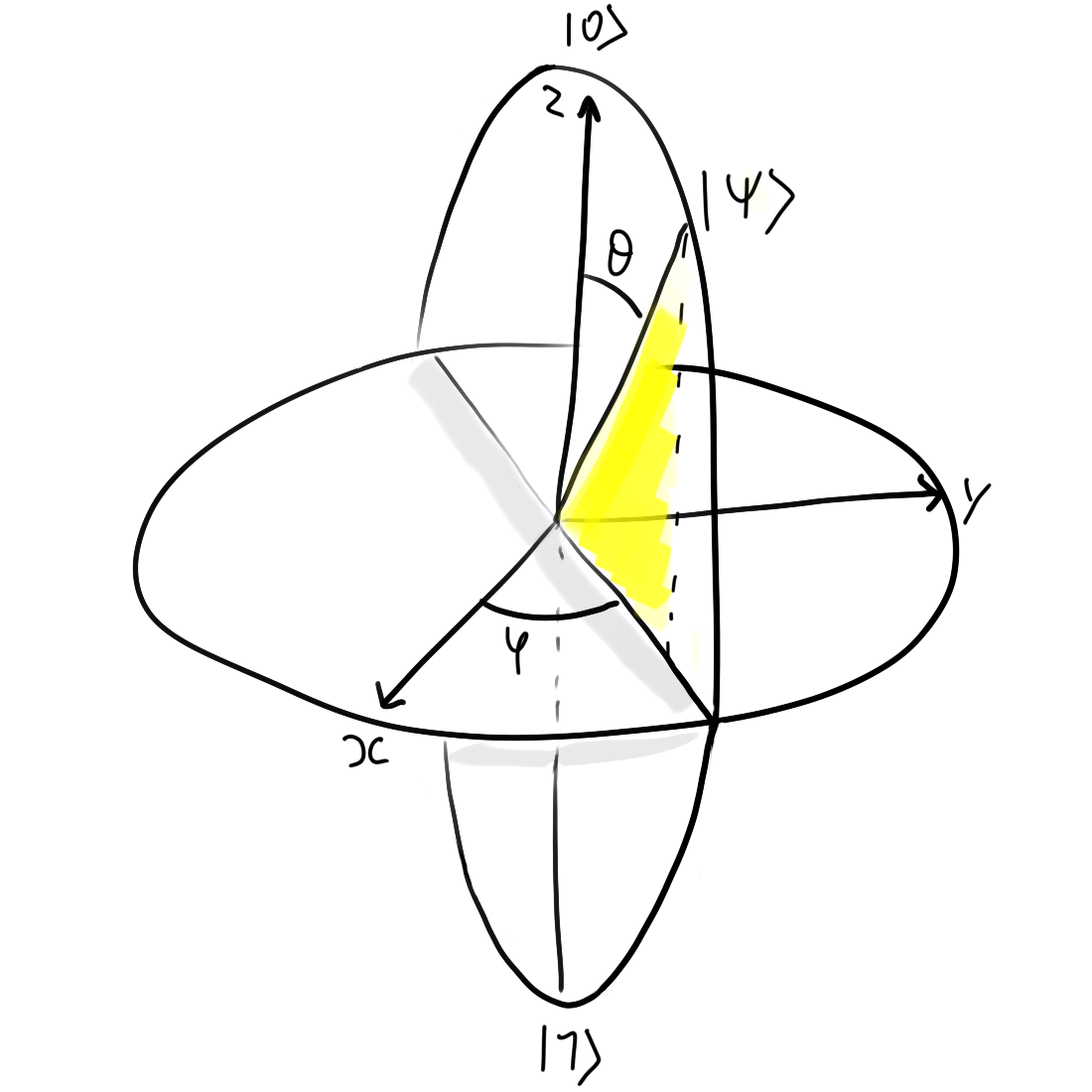
A qbit can have an infinite number of values, we cannot represent it through a Truth Table. However, they can be represented as a matrix.
There are an uncountable infinite number of quantum gates, but here are the most interesting one.
Identity
$$
\left< I | \Psi \right> = \left| \Psi \right>
$$
Or, using matrix representation:
$$
\begin{bmatrix}
1 & 0 \cr
0 & 1
\end{bmatrix}
\cdot
\begin{bmatrix}
\alpha \cr
\beta \cr
\end{bmatrix}
=
\begin{bmatrix}
\alpha \cr
\beta \cr
\end{bmatrix}
$$
Pauli X
Equivalent of NOT gate, noted \(\sigma_x\):
$$
\left< \sigma_x | 0 \right> = \left| 1 \right>
\\
\left< \sigma_x | 1 \right> = \left| 0 \right>
$$
Using matrix representation:
$$
\begin{bmatrix}
0 & 1 \cr
1 & 0
\end{bmatrix}
\cdot
\begin{bmatrix}
\alpha \cr
\beta \cr
\end{bmatrix}
=
\begin{bmatrix}
\beta \cr
\alpha \cr
\end{bmatrix}
$$
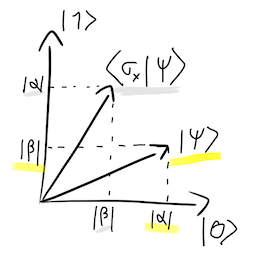
In Bloch Sphere:
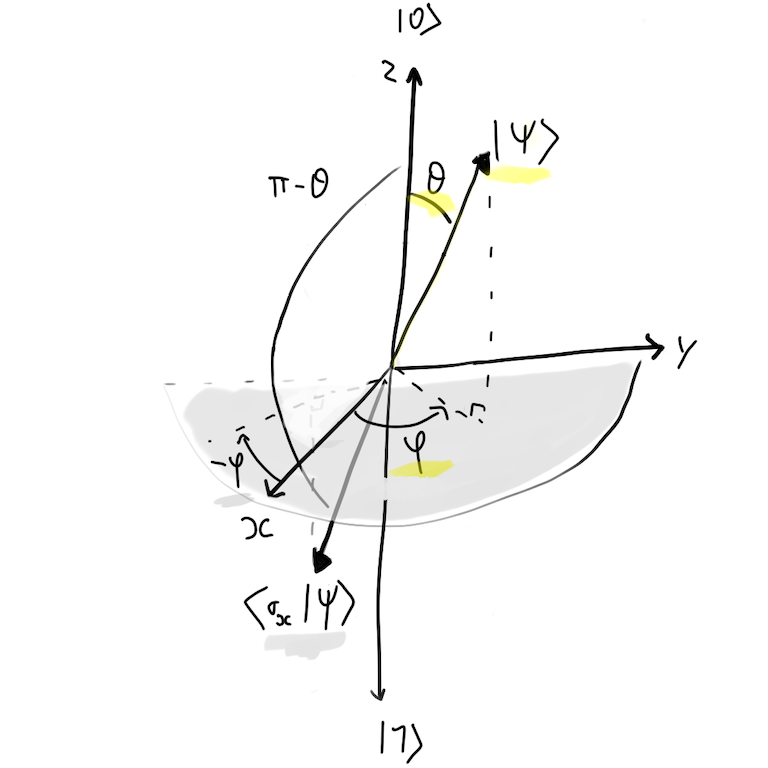
It apply a 180º rotation around X axis, swap α and β probabilities and keep the same phase ϕ.
$$
\begin{align}
\begin{bmatrix}
0 & 1 \cr
1 & 0
\end{bmatrix}
\cdot
\begin{bmatrix}
cos( \frac{\theta}{2}) \cr
e^{i\phi} sin(\frac{\theta}{2}) \cr
\end{bmatrix}
&=
\begin{bmatrix}
e^{i\phi} sin(\frac{\theta}{2}) \cr
cos( \frac{\theta}{2}) \cr
\end{bmatrix}
\\
&=
\begin{bmatrix}
e^{i\phi} cos(\frac{\theta}{2} + \frac{\pi}{2}) \cr
sin(\frac{\theta}{2} + \frac{\pi}{2}) \cr
\end{bmatrix}
\\
&\cong
\begin{bmatrix}
cos(\frac{\theta + \pi}{2}) \cr
e^{-i\phi}sin( \frac{\theta + \pi}{2}) \cr
\end{bmatrix}
\end{align}
$$
Pauli Y
Noted \(\sigma_y\):
$$
\begin{align}
&\left< \sigma_y | 0 \right> = i\left| 1 \right>
\\
&\left< \sigma_y | 1 \right> = -i\left| 0 \right>
\end{align}
$$
Using matrix representation:
$$
\begin{bmatrix}
0 & -i \cr
i & 0
\end{bmatrix}
\cdot
\begin{bmatrix}
\alpha \cr
\beta \cr
\end{bmatrix}
=
\begin{bmatrix}
-i\beta \cr
i\alpha \cr
\end{bmatrix}
$$
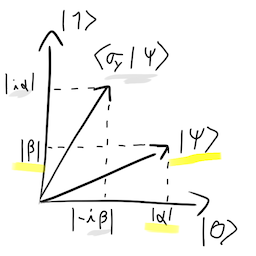
In Bloch Sphere:
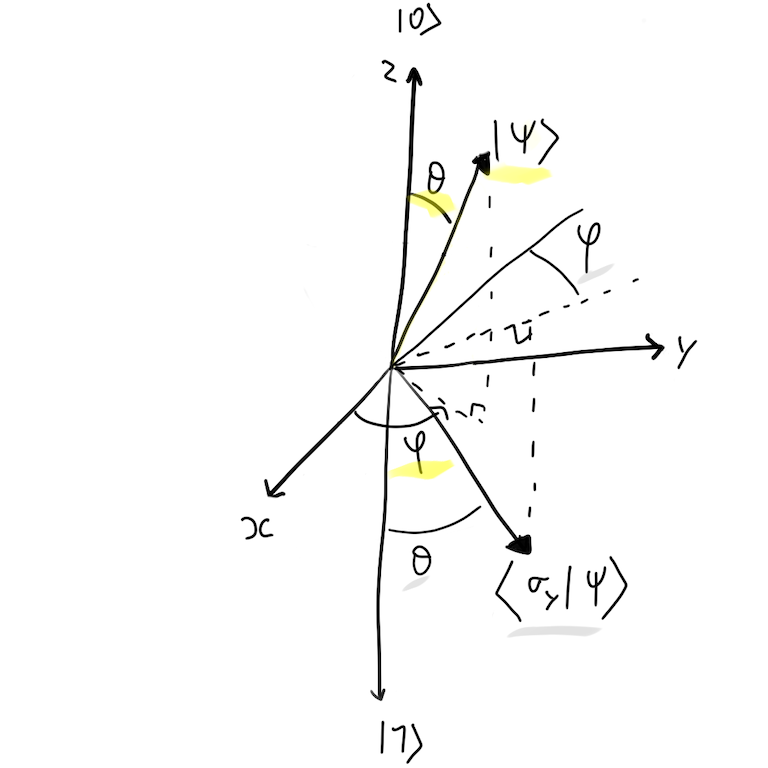
It apply a 180º rotation around Y axis, swap α and β probabilities and shift the phase ϕ.
,
$$
\begin{align}
\begin{bmatrix}
0 & -i \cr
i & 0
\end{bmatrix}
\cdot
\begin{bmatrix}
cos( \frac{\theta}{2}) \cr
e^{i\phi} sin(\frac{\theta}{2}) \cr
\end{bmatrix}
&=
\begin{bmatrix}
-i \cdot e^{i\phi} sin(\frac{\theta}{2}) \cr
i \cdot cos( \frac{\theta}{2}) \cr
\end{bmatrix}
\\
&=
\begin{bmatrix}
e^{i\frac{-\pi}{2}}e^{i\phi} cos(\frac{\pi}{2} - \frac{\theta}{2}) \cr
e^{i\frac{\pi}{2}}sin(\frac{\pi}{2} - \frac{\theta}{2}) \cr
\end{bmatrix}
\\
&=
\begin{bmatrix}
e^{i (\phi - \frac{\pi}{2})}cos(\frac{\pi - \theta}{2}) \cr
e^{i\frac{\pi}{2}}sin(\frac{\pi - \theta}{2}) \cr
\end{bmatrix}
\\
&\cong
\begin{bmatrix}
cos(\frac{\pi - \theta}{2}) \cr
e^{i(\frac{\pi}{2} - (\phi - \frac{\pi}{2}))}sin(\frac{\pi - \theta}{2}) \cr
\end{bmatrix}
\\
&=
\begin{bmatrix}
cos(\frac{\pi - \theta}{2}) \cr
e^{i(\pi - \phi)}sin(\frac{\pi - \theta}{2}) \cr
\end{bmatrix}
\end{align}
$$
Pauli Z
Noted \(\sigma_z\):
$$
\begin{align}
&\left< \sigma_z | 0 \right> = \left| 0 \right>
\\
&\left< \sigma_z | 1 \right> = -\left| 1 \right>
\end{align}
$$
Using matrix representation:
$$
\begin{bmatrix}
1 & 0 \cr
0 & -1
\end{bmatrix}
\cdot
\begin{bmatrix}
\alpha \cr
\beta \cr
\end{bmatrix}
=
\begin{bmatrix}
\alpha \cr
-\beta \cr
\end{bmatrix}
$$
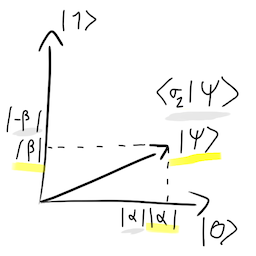
In Bloch Sphere:
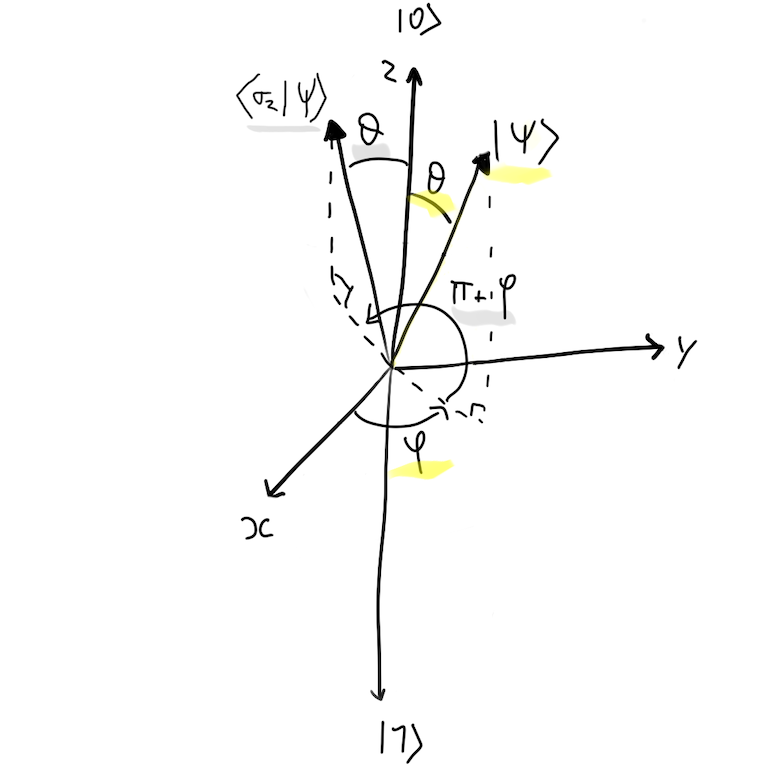
It apply a 180º rotation around Z axis, keep α and β probabilities and flip the phase ϕ.
$$
\begin{align}
\begin{bmatrix}
1 & 0 \cr
0 & -1
\end{bmatrix}
\cdot
\begin{bmatrix}
cos( \frac{\theta}{2}) \cr
e^{i\phi} sin(\frac{\theta}{2}) \cr
\end{bmatrix}
&=
\begin{bmatrix}
cos( \frac{\theta}{2}) \cr
-e^{i\phi} sin(\frac{\theta}{2}) \cr
\end{bmatrix}
\\
&=
\begin{bmatrix}
cos( \frac{\theta}{2}) \cr
e^{i\pi}e^{i\phi} sin(\frac{\theta}{2}) \cr
\end{bmatrix}
\\
&=
\begin{bmatrix}
cos( \frac{\theta}{2}) \cr
e^{i(\phi + \pi)} sin(\frac{\theta}{2}) \cr
\end{bmatrix}
\end{align}
$$
Hadamard
Hadamard gate is used to create a superposition state given a basis state.
Noted \( H :\)
$$
\begin{align}
&\left< H | 0 \right> = \frac{\left| 0 \right> + \left| 1 \right>}{\sqrt{2}} = \left|+\right>
\\
&\left< H | 1 \right> = \frac{\left| 0 \right> - \left| 1 \right>}{\sqrt{2}} = \left|-\right>
\end{align}
$$
Using matrix representation:
$$
\frac{1}{\sqrt{2}}
\begin{bmatrix}
1 & 1 \cr
1 & -1
\end{bmatrix}
\cdot
\begin{bmatrix}
\alpha \cr
\beta \cr
\end{bmatrix}
=
\frac{1}{\sqrt{2}}
\begin{bmatrix}
\alpha + \beta \cr
\alpha - \beta \cr
\end{bmatrix}
$$
Let's note that:
$$
\begin{align}
&H = XY^{\frac{1}{2}} = R_x(\pi)R_y(\frac{\pi}{2})
\\
&H = Y^{-\frac{1}{2}}X = R_y(-\frac{\pi}{2})R_x(\pi)
\\
&H = Y^{\frac{1}{2}}Z = R_y(\frac{\pi}{2})R_z(\pi)
\\
&H = ZY^{-\frac{1}{2}} = R_z(\pi)R_y(-\frac{\pi}{2})
\\
&H = H^{-1}
\end{align}
$$
In Bloch Sphere:
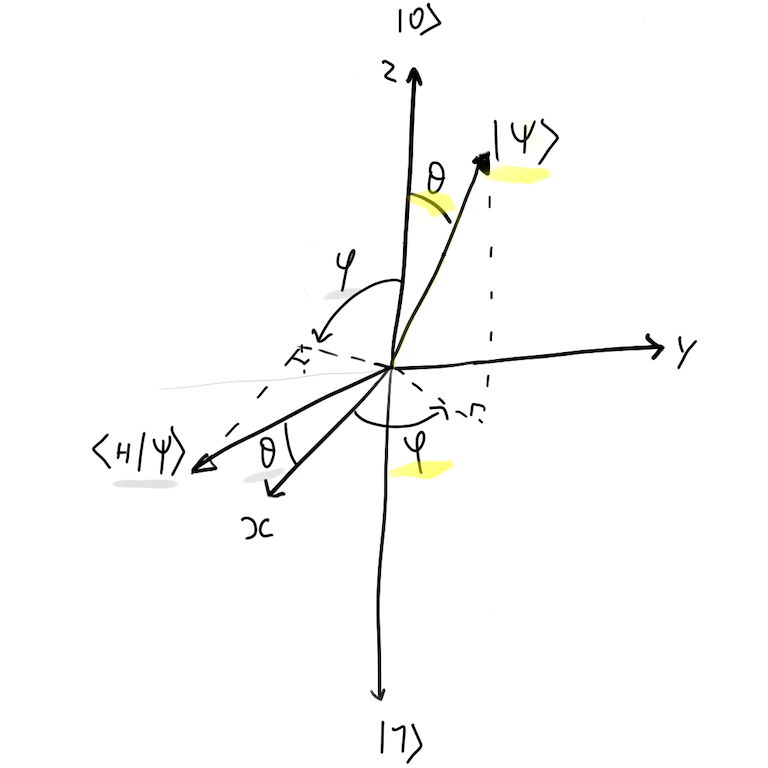
It apply a 90º rotation around the Y-axis, followed by a 180º rotation around the X-axis.
$$
\begin{align}
\frac{1}{\sqrt{2}}
\begin{bmatrix}
1 & 1 \cr
1 & -1
\end{bmatrix}
\cdot
\begin{bmatrix}
cos( \frac{\theta}{2}) \cr
e^{i\phi} sin(\frac{\theta}{2}) \cr
\end{bmatrix}
&=
\begin{bmatrix}
cos( \frac{\theta}{2}) + e^{i\phi} sin(\frac{\theta}{2}) \cr
cos( \frac{\theta}{2}) - e^{i\phi} sin(\frac{\theta}{2}) \cr
\end{bmatrix}
\\
\end{align}
$$
Takeaways
- Single Qbit Quantum gates change the orientation of QBit on the Bloch sphere. They act on \(\alpha\) and \(\beta\) probability (through acting on \(\theta\) angle) and on phase \(\phi\).
- When there are only 2 logic gates that can act on a single bit (Identity and NOT), there is an infinite number of Quantum gates that can act on a single qbit.
- PauliX gate is the equivalent of NOT gate.
- Hadamard gate is classically used to create superposition state.